접근 가능성하고 S5 이런게 뭔지 설명해 달라고 해서 글을 쓰면
https://www.chuing.net/zboard/zboard.php?id=mvs&no=214669&cpage=1#commentHidden1438062
이 글에서 누가 물어봐서 내가 답글 달아준 내용을 복붙한 것을 기반으로 약간의 추가한 이미지를 통한 설명도 넣음
Q : 혹시 S5, S4, B, T, D, K의 정의가 뭔지 간단히라도 설명해줄 수 있으심?
가능세계 개념은 어느정도는 이해가 가는데 이 개념들이 뭔지 모르겠어서..
A :
K, K4, D, T, KB, B, S4, S5은 정규 양상 논리의 공리들인데 논리식에 양상 연산자가 중첩되어 쓰였을 때 이것의 의미를
가능세계론으로 해석할 때 접근 가능성 관계(accessibility relation)를 통해서 이해할 수 있고
접근 가능성 관계는 가능세계 간의 관계를 말하고 관계(relation)는 수학에서 말하는 그 관계임.
접근 가능성 관계는 여러가지가 있음(반사관계, 대칭관계, 추이관계, 연속관계, 유클리드 관계 등등)
가능세계 w1에서 w2로 접근 가능한 관계가 있는 경우에는 w1에서 w2로 접근(이동)하는데 이때 접근한다는 것이
어떤 물리적인 공간적, 시간적 접근을 하는 것은 아님. 기본적으로 가능세계들 끼리는 시공적으로 독립이 되어있거든
그렇다면 접근한다 혹은 이동한다라는 것은 무슨 의미냐?
어떤 세계 w1에서 세계 w2로 접근(이동)한다는 것은 세계 w1에서 보았을 때, 세계 w2가 가능하다와 같은
논리적 가능성이나 어떤 명제가 특정 가능세계에서 참인지 여부를 평가할 때, 해당 세계에서 접근할 수 있는
다른 세계를 참조하여 고려할 수 있는 등의 논리적 평가의 맥락에서 사용되는 말임
그래서 어떤 세계에서 '접근 가능하다'는 것은 가령 현실세계를 기준으로 잡았을 때 현실세계에서
어떤 명제의 참 거짓에 관하여 고려할 때 대체세계로 참조할 수 있다고 생각하면 될듯
예컨데 내일 6시에 출근을 해야하는데 지각을 하는 가능세계, 정시출근을 하는 가능세계 둘다
현실세계에서 봤을 때 가능한 세계이고 접근 가능한 세계일거임
이 접근 가능한 세계가 우리가 사는 현실과 크게 괴리가 있다고 보기는 어렵겠지?
왜냐면 내가 내일 회사에 지각하냐? 라는 명제에 대해서 현실세계 대신에 저 두가지 가능성의 세계로 대체해서
각각의 명제를 평가를 할 때 접근 가능한 두 세계가 저 지각에 대한 사건을 제외하고 나머지는 현실과 거의 똑같다고
상정을 해야지 현실에서 아직 일어나지 않은 가능성의 세계로 현실을 대체해서 평가를 하는게 의미가 있으니까
어떻게 보면 세계 사이의 논리적 유사성과도 비슷한 측면이 있다고 할 수도 있을듯
K, T, S5, S4, B, KB, D 등의 각각의 공리는
가능세계들이 필수로 만족해야 하는 접근 관계를 요구하는게 다른데
반사성 : 모든 세계는 반드시 자기 자신으로 접근 가능하다.
(자기 자신을 항상 참조할 수 있음)
대칭성 : 임의의 가능세계 w1에서 w2로 접근이 가능하면 반드시 w2에서도 w1으로 접근할 수 있다.
(항상 대칭적으로 양방향 접근이 가능함)
추이성 : 임의의 가능세계 w1에서 w2로 접근이 가능하고 w2에서 w3로 접근이 가능하면 반드시 w1에서 w3로 접근할 수 있다.
(비유적으로는 친구의 친구는 친구이다 같이 연쇄적으로 접근이 가능하면 중간과정을 생략가능)
연속성 : 임의의 가능세계는 적어도 하나 이상의 접근 가능한 세계가 존재한다.
유클리드성 : 임의의 가능세계 w1에서 w2로 접근이 가능하고 w1에서 w3로 접근이 가능하면 w2에서 w3로 접근이 가능.
(같은 출발점을 가진 가능세계들은 서로 연결됨)
S5는 반사성, 대칭성, 추이성을 만족해야 할 것을 요구하며 유클리드 관계는 대칭성과 추이성을 통해서 유도됨
그리고 반사성을 가지면 당연히 연속성도 만족함 자기자신이라는 접근 가능한 세계가 존재하니까
반사성, 대칭성, 추이성을 모두 만족해야하는 S5에서는 어떤 가능세계에서 시작하던 S5의 임의의 가능세계로
항상 접근할 수 있음. 즉 S5의 모든 가능세계는 반드시 상호접근이 가능함
S5에서는 접근할 수 없는 가능세계가 없는데 S5보다 더 접근 관계에 대한 제약이 약하다면 어떤 가능세계에서는 접근이
불가능한 그런 세계도 상정이 가능할거임 즉 접근 관계에 대한 제약조건이 적을수록 상정할 수 있는 세계가 풍부해짐
반사성을 만족할 필요가 없다면 자기자신을 참조할 수 없는 세계도 있을거고
대칭성을 만족할 필요가 없다면 양방향이 아닌 한쪽에서만 접근할 수 있는 경우도 있을거고
추이성을 만족할 필요가 없다면 연쇄적으로 접근이 가능하다고 해서 떨어진 세계와 직접 접근하는건 불가능 할 수 있음
연속성을 만족할 필요가 없다면 그 어떤 접근 가능한 세계도 존재하지 않는 가능세계가 있을 수 있겠지
접근 관계의 제약이 작은 것을 기준으로 순위를 매기면 K(접근 관계에 대한 조건이 없음) > D(K에 연속성 추가), K4(K에 추이성 추가), KB(K에 대칭성 추가) > T(D에 반사성 추가) > B(T에 대칭성 추가), S4(T에 추이성 추가) > S5(S4에 대칭성를 추가 또는 B에 추이성을 추가) 이렇게 될거임
도식으로 보면 이런 느낌
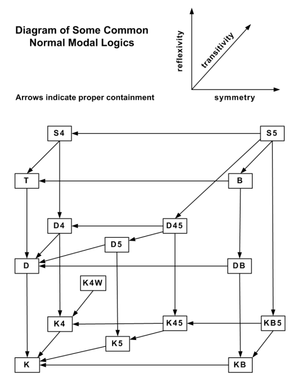
도식에서 X축은 대칭성, Y축은 추이성, Z축은 반사성으로 보면 될거 같음
K에서 시작해서 반사성(reflectivity) 방향으로 조건을 추가하면 T를 향해 나아감
K에서 시작해서 대칭성(symmetry) 방향으로 조건을 추가하면 KB를 향해 나아감
K에서 시작해서 추이성(transitivity) 방향으로 조건을 추가하면 K4를 향해 나아감
그리고 이것들을 다 적용하면 S5를 향해 나아가는 것도 도식으로 볼 수 있고
가장 근본이 되는 K가 정규 양상논리의 시작점 같은걸로 보면됨
추천
[신고]